4. Expression

An expression is composed of integers, identifiers, and integer mathematical operations.

4.1. Operators

Operation	Symbol	Usage	Associativity
exponentiation	^	expr ^ expr	right
multiplication	*	expr * expr	left
division	/	expr / expr	left
remainder	%	expr % expr	left
addition	+	expr + expr	left
subtraction	-	expr - expr	left

Assertion: All exponents are \(\geq 0\). (nonnegative-exp)

Clarification: The % operator is remainder not modulus. (rem-not-mod)

Clarification: Division is integer division. (int-div)

4.2. Valid Expressions

Valid formats for expressions are

(<expr>)
<expr> <op> <expr>
<int>
<id>

• expr is an expression.

• int is an integer.

• id is the identifier of a variable.

Assertion: All expressions will result in a value that fits in a 32 bit signed integer. (expression-size)

Assertion: No expression will contain a division by 0. (zero-divide)

Examples of valid expressions are

i * 2 * 10 + 4
2 ^ 4 * 5

4.3. Precedence

Precedence determines what order operations are evaluated in. Precedence works as defined in the following table:

Precedence	Operations
HIGHER	^
	* / %
LOWER	+ -

The higher the precedence the sooner the value should be evaluated. For example, in the expression

1 + 2 * 3

2 * 3 should be evaluated before 1 + 2. This is because multiplication, division, and remainder have higher precedence than addition and subtractions.

4.4. Associativity

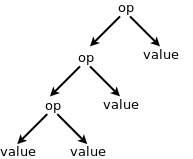
When parsing expressions associativity determines in what order operators of the same precedence should be evaluated in. For example:

1 / 2 * 3

In this example both division and multiplication have the same precedence; associativity determines which operations are evaluated first. Left associative operations will form a parse tree like this:

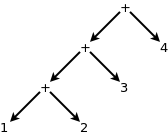
An example of one of these operations is addition. Lets say we have the following expression:

1 + 2 + 3 + 4

Because addition is left associative it will form the following parse tree:

An operation in such a parse tree can only be evaluated when all the operands are leaves. Thus, in this parse tree, the expression 1 + 2 is evaluated first and then the result of this evaluation replaces the subtree for the expression 1 + 2 to create the following tree.

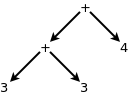
Next, the expression 3 + 3 is evaluated, making

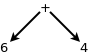
Most operations used in this assignment are left associative, but there are also operations that are right associative and take this format:

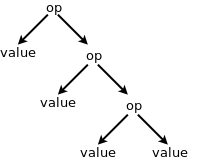
An example of a right-associative operation is the exponentiation operation represented by the symbol ^. For example

2 ^ 3 ^ 4 ^ 5

should be evaluated as: \(2 ^ {3 ^ {4 ^ {5}}}\)

In order for this expression to be evaluated correctly the following parse tree must be generated

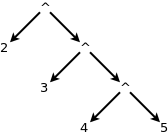
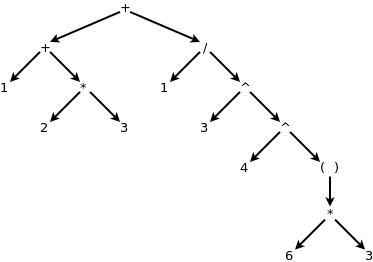
For a more complex example consider the expression:

1 + 2 * 3 + 1 / 3 ^ 4 ^ (6 * 3)

which generates the following parse tree: